Introduction
Long division is a method of performing division that uses the traditional pencil-and-paper approach. It’s a useful tool for dividing larger numbers and can help you improve your understanding of fractions. Here, we’ll explain what 5 divided by 3 using long division looks like, as well as provide you with some tips on how to solve it correctly. Keep reading to learn more about this important math skill and how it can help you understand fractions better.
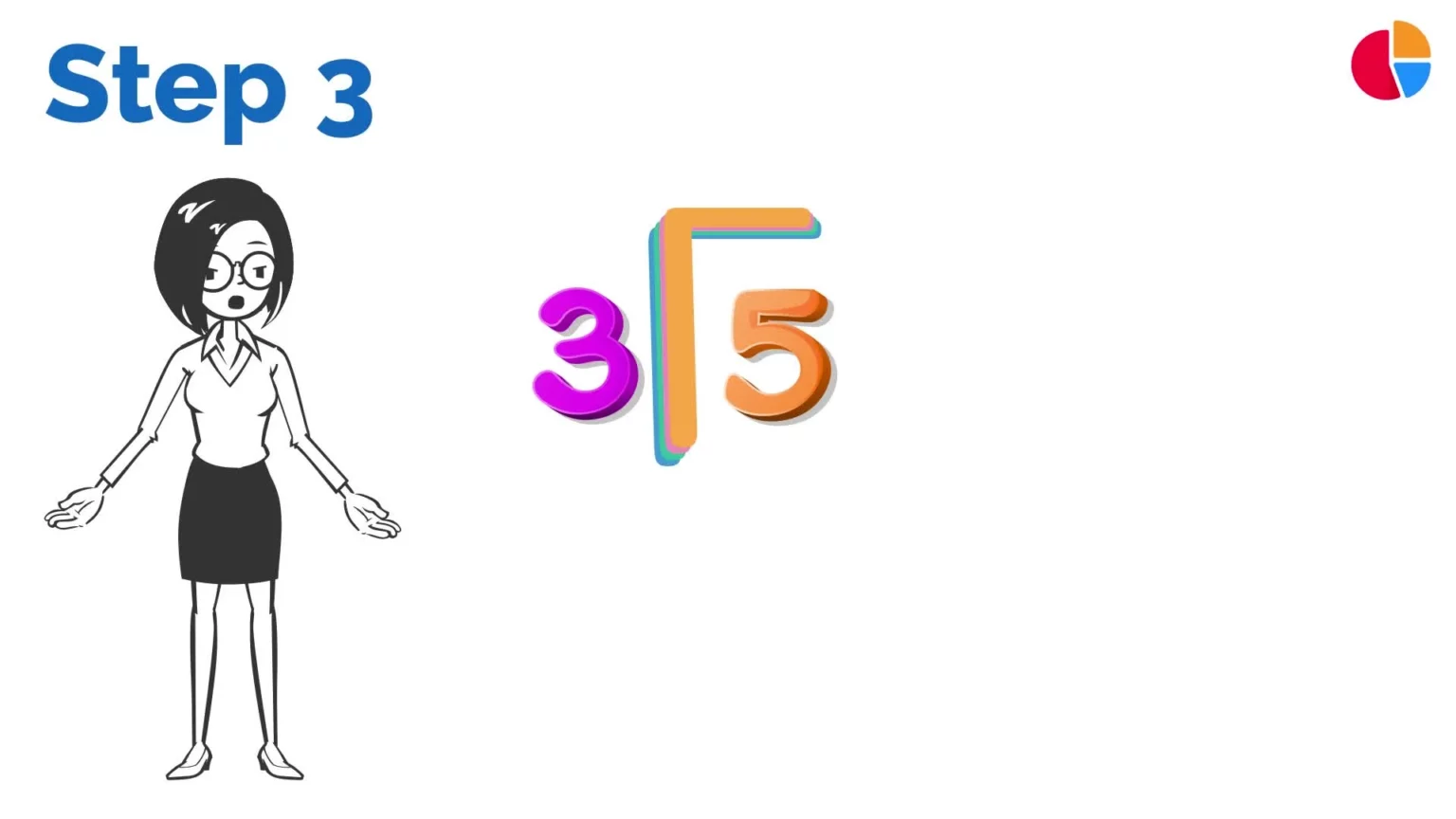
What is 5 divided by 3 using long division?
5 divided by 3 using long division is pretty simple. You just need to follow these steps:
1. Write down the dividend (5) and the divisor (3) with a division sign between them.
2. Bring down the first number of the dividend (5) to be the first number in the quotient.
3. Divide 5 by 3 to get 1 with a remainder of 2. Write this quotient next to the 5 like so: 15
4. Put the 2 over 3 and bring down the next number in the dividend (15), making it become 25.
5. Divide 25 by 3 to get 8 with a remainder of 1. Write 8 next to the 15 like so:815
6. Put 1 over 3 and bring down the last number in the dividend (8), making it become 81.
7. Divide 81 by 3 to get 27 with a remainder of 0. Write 27 next to 815 like so:81527
Since there is no remainder, we are done! The answer is 27/3 or 9 if you’re looking for an improper fraction
The steps to divide 5 by 3 using long division
When dividing fractions, we use the same principles as whole number division. In long division, we divide the dividend (5) by the divisor (3). This process is also called “measurement division” because we are essentially measuring out how many times the divisor goes into the dividend.
We begin by writing the dividend (5) above the line and the divisor (3) below the line. We then divide 5 by 3 to get 1 with a remainder of 2. We write this answer as follows:
5 | 3
— —
1 R2
This means that 1 times 3 equals 3 and that 2 goes into 5 once with a remainder of 2. We bring down the next number in the dividend (the 2 from above), which gives us a new problem of 22 divided by 3. Again, we divide 22 by 3 to get 7 with a remainder of 1 and write this answer underneath our first:
5 | 3
— —
1 R2 7R1
—
1
Why is the answer 1 2/3 and not 1 1/3?
When you divide fractions, you are essentially solving for how many times one fraction can go into another. In the case of 1 2/3 divided by 1 1/3, that’s equivalent to asking how many times 1 2/3 can go into 1 1/3.
The answer, it turns out, is 1 2/3 can go into 1 1/3 once, with a remainder of 0. So the answer to the division problem is 1 2/3 divided by 1 1/3 is equal to 1, with a remainder of 0.
Conclusion
In this article, we have discussed the long division process for solving a fractional equation. We explained how to find the answer of 5 divided by 3 using long division and showed an example of it in action. With this method, you can easily solve any fraction without having to break down the whole number or use complex calculations. It’s a simple yet effective way to quickly calculate fractions – no matter how large or small they are!